Syllabus for Quantum Mechanics
-
(Physics 115B, UC Davis, Fall 2010)
- Review
- Spin
- Quantum Mechanics in 3D
- Shrodinger Eq, in Spherical Coordinates
- Hydrogen Atom
- Angular Momentum
- Spin revisited
- Clebsch-Gordan Coefficients
- Identical Particles
- Two Particle Systems
- Identical Bosons and Fermions
- Atoms
- Fermi Energy
- Quantum Statistical Mechanics
- Time-Independent Perturbation Theory
- Nondegenerate
- Degenerate
- Fine structure
- Zeeman effect
- Hyperfine Splitting
- Variational Method
- bounding the ground state energy
- ionized hydrogen molecule
- Time-dependent Perturbation Theory
- Two-level Systems
- Emission and Absorption of Radiation
- Spontaneous Emission
- Scattering
- Partial Wave Analysis
- Phase Shifts
- Born Approximation
- How does a Quantum Computer work and what is the current progress on it? (Answered in lecture 23.)
- Why are Quantum Mechanics and General Relativity considered to be incompatible and how are physicists trying to solve this problem? (Answered in lecture 17.)
- How does quantum teleportation work? Is it controllable or is it random? How can we use it and what does it imply for future physics? (Answered in lecture 20.)
- I have heard that when a particle is taking a path through space it is actually taking ALL paths simultaneously. My question is how is this possible and can we see some of the calculations done using this concept? (Answered in lecture 24.)
- Why are only fermions subject to the Pauli Exclusion Principle and not bosons? Is there some deeper physical principle or is it just another axiom of quantum mechanics? (Answered in lecture 10.)
- Problem Set 1 due Oct. 1
- Problem Set 2 due Oct. 4
- Problem Set 3 due Oct. 8
- Problem Set 4 due Oct. 12
- Problem Set 5 due Oct. 15
- Problem Set 6 due Oct. 19
- Problem Set 7 due Oct. 22
- Problem Set 8 due Oct. 29
- Problem Set 9 due Nov. 2
- Problem Set 10 due Nov. 5
- Problem Set 11 due Nov. 9
- Problem Set 12 due Nov. 12
- Problem Set 13 due Nov. 18
- Problem Set 14 due Nov. 19
- Problem Set 15 due Nov. 23
- Problem Set 16 due Nov. 30
- Lecture 1: Principles of QM applied to Spin
- Lecture 2: Schrödinger Eq. in 3D
- Lecture 3: Spehrical Harmonics
- Lecture 4: Hydrogen Atom
- Lecture 5: Hydrogen Spectrum and Angular Momentum Commutators
- Lecture 6: Angular Momentum Raising and Lowering Operators
- Lecture 7: Spin
- Lecture 8: Addition of Angular Momentum
- Lecture 9: Atoms
- Lecture 10: Free Electron Gas
- Lecture 11: Quantum Statistical Mechanics
- Lecture 12: Quantum Statistical Mechanics: Applications
- Lecture 13: Perturbation Theory
- Lecture 14: Perturbation Theory: Examples
- Lecture 15: Degenerate Perturbation Theory
- Lecture 16: Degenerate Perturbation Theory: Examples
- Lecture 17: Fine Structure
- Lecture 18: Hyperfine Structure and the Stark Effect
- Lecture 19: Variational Method
- Lecture 20: Time Dependent Perturbation Theory
- Lecture 21: Interaction with Light
- Lecture 22: Hydrogen Decay
- Lecture 23: NMR and Scattering
- Lecture 24: Quantum Scattering
- Lecture 25: Born Approximation
- Lecture 26: Yukawa Potential
- Lecture 27: Doping Semiconductors
- Lecture 1: Principles of QM applied to Spin
- Lecture 2: Schrödinger Eq. in 3D
- Lecture 3: Spehrical Harmonics
- Lecture 4: Hydrogen Atom
- Lecture 5: Hydrogen Spectrum
- Lecture 6: Angular Momentum Raising and Lowering Operators
- Lecture 7: Spin
- Lecture 9: Atoms
- Lecture 10: Free Electron Gas
- Lecture 11: Quantum Statistical Mechanics
- Lecture 12: Quantum Statistical Mechanics: Applications
- Lecture 13: Perturbation Theory
- Lecture 14: Perturbation Theory: Examples
- Lecture 17: Fine Structure
- Lecture 18: Hyperfine Structure and the Stark Effect
- Lecture 19: Variational Method
- Lecture 20: Time Dependent Perturbation Theory
- Lecture 22: Hydrogen Decay
- Lecture 23: NMR and Scattering
- Lecture 26: Yukawa Potential
- SPINS simulation software
- History of the Stern-Gerlach experiment
- Clebsch-Gordan Calculator
- The man behind Bose statistics
- Fermi surfaces
- Magnetic Resonance Imaging
- Discovery of the Hyperfine line
- Atomic Cookies!
- scattering in 2D
- Bloch and Purcell: Nobel Prize in Physics 1952
- Ewen & Purcell
- Quantum encryption sets speed record
Location: 130 Physics
Time: MWF 10:00-10:50 am
Professor: John Terning
email: jterning+115B@gmail.com
Office: 435
Office Hours: Wed. 3 pm
Web Page: /teaching/115B/index.php
Grader: Hai-Ying Cai
email: Hai-Ying Cai
Office: 436
Office Hours: Wed. 5 pm
Course Outline
Textbook: "Introduction to Quantum Mechanics" by D.J. Griffiths
Grading will be based on regular reading assignments, problem sets, two midterms, and a final exam. The grade breakdown will be 10% on reading assignments, 30% on problems sets, 15% on each midterm, and 30% on the final exam
Quantum Questions
As chosen by 115B students, these questions will be answered during the quarter:Assignments
Reading assignments are due one hour before the start of class.
Homework is due on Tuesdays in the grader's mailbox and Fridays at the start of class.
Note 15 % will be deducted per day late for all problem sets, up until the solutions are posted online. If you want to submit a late assignment, please make arrangements with the grader to drop it off.
Lecture Notes
Audio recordings of the lectures are available for downloading directlyor through iTunes.
Slides
First Midterm: Oct. 25
The first Midtern will cover Chapter 4.
out of 25, mean: 16.1, standard deviation: 2.8, median 16, mode 17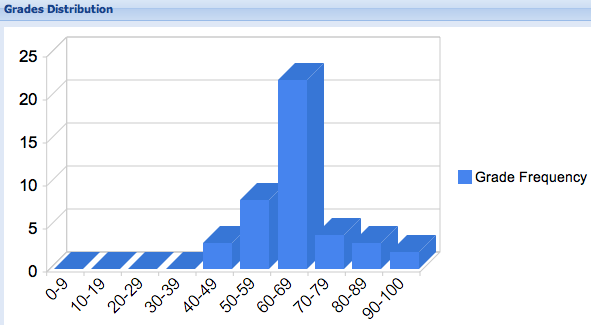
Second Midterm: Nov. 17
The second Midtern will cover Chapter 5 (except for section 5.3.2) and Chapter 6 up to the end of section 6.3.
out of 100, mean: 79.3, standard deviation: 8.6, median 79.5, mode 88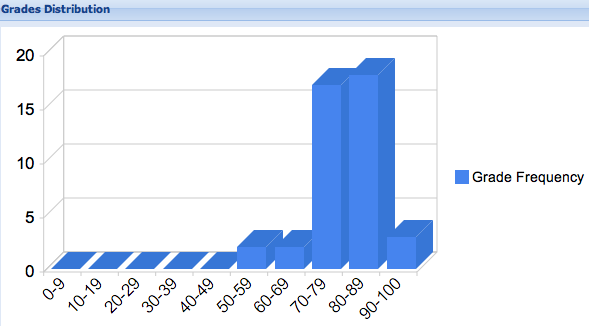
Final: Wed Dec. 8, from 10:30 am to 12:30 pm.
out of 60, mean: 43.7, standard deviation: 7.3, median 45, mode 49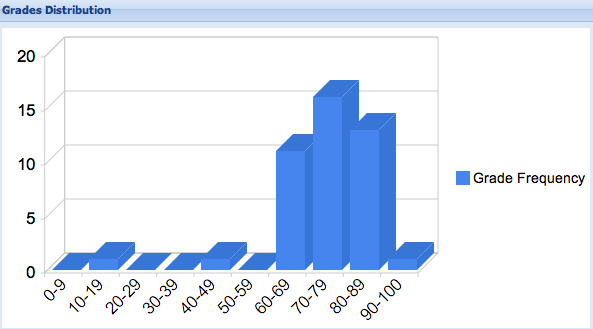
Additional Materials
Other Information
If you have not already done so please review the UC Davis Code of Academic Conduct.
If you need to document a learning disability contact the Student Disability Center.
