Syllabus for Quantum Mechanics

Review
Spin
Quantum Mechanics in 3D
- Shrodinger Eq, in Spherical Coordinates
- Hydrogen Atom
- Angular Momentum
- Spin revisited
- Clebsch-Gordan Coefficients
Identical Particles
- Two Particle Systems
- Identical Bosons and Fermions
- Atoms
- Fermi Energy
- Quantum Statistical Mechanics
Time-Independent Perturbation Theory
- Nondegenerate
- Degenerate
- Fine structure
- Zeeman effect
- Hyperfine Splitting
Variational Method
- bounding the ground state energy
- ionized hydrogen molecule
Time-dependent Perturbation Theory
- Two-level Systems
- Emission and Absorption of Radiation
- Spontaneous Emission
Scattering
- Partial Wave Analysis
- Phase Shifts
- Born Approximation

Quantum Questions

How does a Quantum Computer work and what is the current progress on it? (Answered in lecture 23.)
Why are Quantum Mechanics and General Relativity considered to be incompatible and how are physicists trying to solve this problem? (Answered in lecture 17.)
How does quantum teleportation work? Is it controllable or is it random? How can we use it and what does it imply for future physics? (Answered in lecture 20.)
I have heard that when a particle is taking a path through space it is actually taking ALL paths simultaneously. My question is how is this possible and can we see some of the calculations done using this concept? (Answered in lecture 24.)
Why are only fermions subject to the Pauli Exclusion Principle and not bosons? Is there some deeper physical principle or is it just another axiom of quantum mechanics? (Answered in lecture 10.)

Assignments

Reading assignments are due one hour before the start of class.
Homework is due on Tuesdays in the grader's mailbox and Fridays at the start of class.

Problem Set 1 due Oct. 1
Problem Set 2 due Oct. 4
Problem Set 3 due Oct. 8
Problem Set 4 due Oct. 12
Problem Set 5 due Oct. 15
Problem Set 6 due Oct. 19
Problem Set 7 due Oct. 22
Problem Set 8 due Oct. 29
Problem Set 9 due Nov. 2
Problem Set 10 due Nov. 5
Problem Set 11 due Nov. 9
Problem Set 12 due Nov. 12
Problem Set 13 due Nov. 18
Problem Set 14 due Nov. 19
Problem Set 15 due Nov. 23
Problem Set 16 due Nov. 30

Note 15 % will be deducted per day late for all problem sets, up until the solutions are posted online. If you want to submit a late assignment, please make arrangements with the grader to drop it off.

Lecture Notes

Audio recordings of the lectures are available for downloading directly or through iTunes.

Slides

First Midterm: Oct. 25

The first Midtern will cover Chapter 4.
out of 25, mean: 16.1, standard deviation: 2.8, median 16, mode 17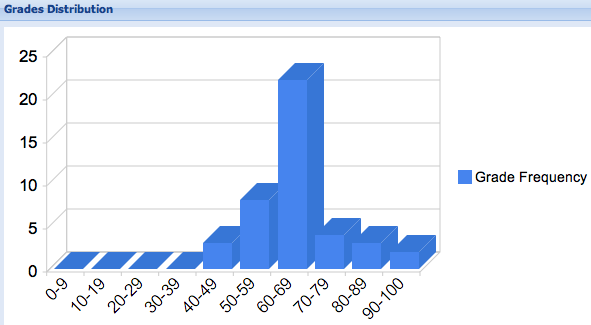

Second Midterm: Nov. 17

The second Midtern will cover Chapter 5 (except for section 5.3.2) and Chapter 6 up to the end of section 6.3.
out of 100, mean: 79.3, standard deviation: 8.6, median 79.5, mode 88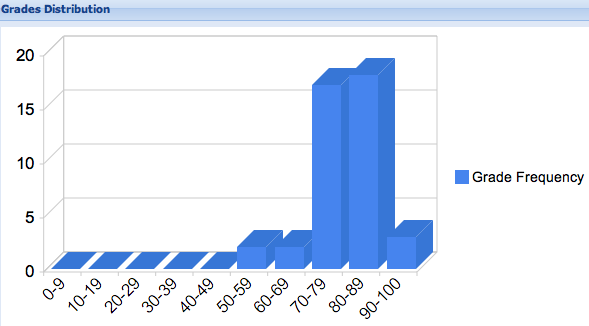

Final: Wed Dec. 8, from 10:30 am to 12:30 pm.

out of 60, mean: 43.7, standard deviation: 7.3, median 45, mode 49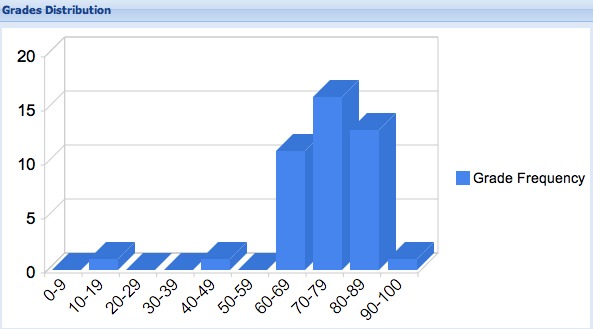

hydrogen video playlist

Additional Materials

Other Information

If you have not already done so please review the UC Davis Code of Academic Conduct.

If you need to document a learning disability contact the Student Disability Center.