Nonlocal Models of Goldstone Bosons ...
Appendix A
Euclidean Space-Time Conventions
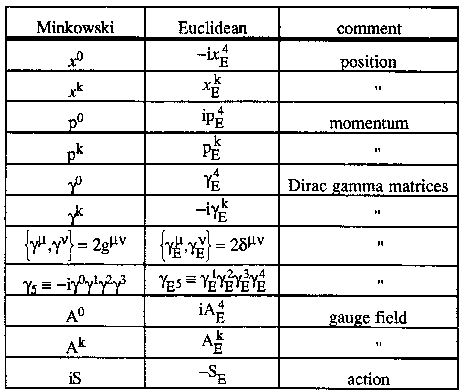
We employ standard conventions for Wick rotating to Euclidean space-
time from Minkoswki space-time [86]. The analytic continuation involved
is summarized in table A.1 [86b]; objects in the first column are replaced
by those in the second.
Table 6.2
Given a propagator in Minkowski space-time:
G(x) = int d^4p/(2 pi)^4 exp(-ip.x) i/(p^2 - m^2 + i epsilon) (A.1)
we can find the Euclidean propagator using Table A.1:
G_E(x) = int d^4p_E/(2 pi)^4 exp(-i(p_E^4 x_E^4 - p_E.x_E)) 1/(p_E^2 + m^2) , (A.2)
note that the exponential does not contain a Euclidean inner product, but
the original Minkowski inner product. However, this is correct; for
example, it gives the correct Euclidean derivative*:
partial_E^mu exp (-i(p_E^4 x_E^4 - p_E.x_E)) = -i p_E^mu exp (-i(p_E^4 x_E^4 - p_E.x_E)
= -i p_E^mu exp (-ip.x ) (A.3)
The exponential of a line integral of a gauge field also involves the
Minkowski inner product, since the gauge field is analytically continued in
the same fashion as a momentum.
Note also that starting with the standard Minkowski definition of the
Fourier transform of a field
phi(x) = int d^4p/(2 pi)^4 e-(ip.x) phi(p), (A.4)
we find for the Euclidean field:
phi_E(x_E) = i int d^4p_E/(2 pi)^4 exp(-ip.x) phi_E(p_E). (A.5)
Finally we note that our dynamical quark mass is defined in Euclidean
space-time such that for a standard local mass term Sigma(p) reduces to Sigma(p) =
m, and Sigma(x-y) is the usual Fourier transform as given by equations A.2 and
A.4.
Footnote:
* The Euclidean derivative partial_E^mu is defined in terms of the contravariant Minkowski derivative partial^mu = (partial^0, -grad^k), so partial_E^mu = (-grad^k, partial^4).

