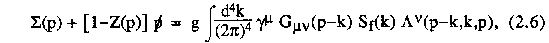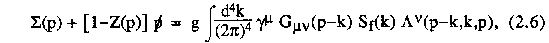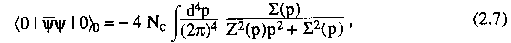Nonlocal Models of Goldstone Bosons ...
Nonlocal Models of Goldstone Bosons in
Asymptotically Free Gauge Theories
by
John Terning
A thesis submitted in conformity with the requirements
for the degree of Doctor of Philosophy at the
University of Toronto
© John Terning
1990
Abstract
We develop a simple model Lagrangian which couples the
pseudo-Goldstone bosons of QCD (pions, kaons, and the eta) to up, down, and
strange quark fields. The model is a nonlocal generalization of the
nonlinear sigma model, which incorporates a momentum dependent dynamical
mass S(p). S(p) is an order parameter for spontaneous chiral symmetry
breaking, and the Goldstone bosons are included as fluctuations of this
order parameter in a manner consistent with global chiral symmetry. No
kinetic energy terms or self-interactions for the Goldstone bosons are
introduced, instead these arise dynamically. Explicit chiral symmetry
breaking effects are also introduced by including current quark masses and
external electroweak gauge fields. By integrating out the quark fields we
obtain a chiral Lagrangian, including the Wess-Zumino term. The
dynamical quark mass acts as a natural regulator, thereby making the
calculations finite. All low energy parameters are expressed in terms of
integrals of S(p). The results are relatively insensitive to the precise form
of S(p), as long as S(p) has the asymptotic behaviour required by QCD.
We use physical values for masses and decay constants (m_pi^0, m_K^+, m_K^-,
m_eta, f_pi, and f_K) to determine the five parameters of our model: the
dynamical quark mass, the quark condensate, and the three current quark
masses. We obtain the 14 parameters of the effective chiral Lagrangian
and find that they are in good agreement with the experimental values.
Acknowledgements
I would like to thank John Moffat, Nathan Isgur, Kevin Dooley, Mark
Sutherland, Daryl Scora, Colin Morningstar, and Karl Verbeek for helpful
discussions. Karl also gave me invaluable computer tutorials and lent me
his computational expertise. I would also like to thank Bob Holdom for
being a great thesis advisor. Finally, I must thank Paul Geiger, Cathy
Reader, and Eric Swanson for innumerable, lengthy, and inspiring
discussions and for interminable proof-reading.
To Donna.
The only truths that are useful are instruments to be thrown away.
- Umberto Eco
Table of Contents
1. Introduction
1.1 - Overview and Outline
2. QCD and Spontaneous Chiral Symmetry Breaking
2.1 - QCD
2.2 - Spontaneous Chiral Symmetry Breaking
2.3 - QCD at Low Energies
3. A Model for Massless QCD
3.1 - Motivation for the Model
3.2 - Ward-Takahashi Identities
3.3 - Comparison With Other Models
3.4 - The Effective Chiral Lagrangian
3.5 - Non-Minimal Models
3.6 - The Effective Chiral Lagrangian at Fourth Order
4. Quark Mass Effects
4.1 - Mass Corrections to the Order Parameter
4.2 - Mass Corrections to the Effective Chiral Lagrangian
4.3 - The Effective Chiral Lagrangian to Fourth Order
4.4 - Mass Corrections to the Quark Self-Energy
5. Electroweak Effects
5.1 - Path Exponentials
5.2 - The Gauged Nonlocal Mass
5.3 - Photons and Goldstone Bosons
5.4 - Electromagnetic Form Factors
5.5 - Non-Abelian Gauge Fields
5.6 - Radiative Weak Decays
6. Comparison with Experiment
6.1 - Matching Conditions
6.2 - Parametrizing the Dynamical Mass
6.3 - Fitting to Masses and Decay Constants
6.4 - Pion Scattering Lengths
7. The Techni-Higgs
7.1 - Scale Invariance
7.2 - Technicolour
7.3 - A Local Dilaton Model
7.4 - A Simple Nonlocal Dilaton Model
8. Conclusions
8.1 - Summary and Speculations
Appendix A
Euclidean Space-Time Conventions
Appendix B
Computer Results
References
Chapter 1
Introduction
1.1 - Overview and Outline
The aim of this thesis is to study spontaneous chiral symmetry breaking
in asymptotically free gauge theories, in particular, we focus on quantum
chromodynamics (QCD) and technicolour theories. Specifically, a model is
developed which makes use of the quark self-energy as a nonlocal order
parameter associated with the spontaneous chiral symmetry breaking. The
Goldstone bosons that must be present are then naturally included as local
fluctuations of this order parameter. It is then possible, using the path
integral formulation of quantum field theory, to functionally integrate out
the quarks, thereby obtaining an effective action for the remaining degrees
of freedom, the Goldstone bosons.
The idea that Goldstone bosons can be considered as fluctuations of the
order parameter is common in condensed matter physics. A familiar
example is that of the Heisenberg ferromagnet [1].
The model Hamiltonian
written down by Heisenberg is invariant under a position-independent
rotation of the spins, but none of the infinite set of ground states of the
system are invariant: in any particular ground state all the spins point in
some arbitrary direction (the z-axis). It can be shown explicitly that such a
system has gapless (the condensed matter analogue of massless) excitations
as expected from Goldstone's theorem [2].
If the spins are given a position
dependent rotation that is slowly varying with respect to the lattice spacing,
then locally each piece of the ferromagnet is approximately in some ground
state. Since there are no long-range interactions in the Hamiltonian, the
energy of such a state can be brought arbitrarily close to the ground state
energy by letting the wavelength of the spin rotation become longer and
longer. The collection of eigenstates with spatial variations in spin
alignment and arbitrarily small energies are called spin-waves. An order
parameter for this system is the expectation value of the z-component of
the spin averaged over a group of spins. Local fluctuations of this order
parameter about its ground state value correspond to superpositions of
spin-waves. The introduction of Goldstone boson fields as fluctuations of
an order parameter in our model is motivated by this analogy in condensed
matter physics*.
Chapter 2 reviews chiral symmetry breaking in QCD and the
phenomenological Lagrangian technique. Through the work of Weinberg
[4], Coleman, Callan, Wess, and Zumino [5] one can easily write down a
phenomenological Lagrangian which represents the low-energy behaviour
of the Goldstone bosons associated with a particular spontaneously broken
(or hidden) symmetry. For this Lagrangian to involve only Goldstone
bosons requires that any other particles which interact strongly with the
Goldstone bosons be heavier than the Goldstone bosons. The form of the
phenomenological Lagrangian is then determined by symmetry
considerations, while the coefficients of the various terms must be fit to
experiment. If one had a chirally symmetric Lagrangian which modeled
the underlying dynamics, the effective action obtained by integrating out
the fields other than the Goldstone bosons must correspond to the
appropriate phenomenological Lagrangian. However, the coefficients of
the various terms would be determined by the properties of the underlying
model.
For the case of QCD it is well known that the pseudoscalar octet mesons
have the properties required of almost-Goldstone bosons of spontaneously
broken chiral symmetry; this is borne out by lattice Monte Carlo
simulations [6].
The appropriate phenomenological Lagrangian which
describes the low energy behaviour of pi's, K's and the eta, is called a chiral
Lagrangian. Chapter 3 explains our model for low energy QCD and our
motivation for the specific form the Lagrangian takes. The model can be
tested by comparing the experimentally determined coefficients (like the
pion decay constant F_pi) in the chiral Lagrangian to those in the effective
action derived from the model. However, the coefficients in the effective
action depend on integrals involving the quark self-energy, which is
unknown. Instead, we first compare the integral expression we obtain for
F_0 (the pion decay constant in the limit that the current quark masses
vanish) to another calculation of F_0 due to Pagels and Stokar
[7]. We also
compare our result for the coefficient of the Wess-Zumino term with the
known coefficient [25].
To make further comparisons with QCD requires the introduction of
explicit symmetry breaking, that is, quark masses and electroweak gauge
fields. These are described in chapters 4 and 5 respectively. The
introduction of quark masses is relatively simple. The major complication
is that the self-energy (the order parameter) can depend on the quark
masses. The introduction of an electromagnetic field (i.e., the introduction
of local gauge invariance) in a nonlocal model can be done formally, but
calculations become quite awkward. They are however doable, and give a
prediction for the electromagnetic charge radius of the pion. Weak decays,
like págen, can be determined in a similar manner.
In chapter 6 our results are compared with experiment. Using a crude
approximation for the self-energy we can predict the 14 parameters of the
chiral Lagrangian (to fourth order in an energy expansion) with the 5
parameters in our model. In addition, our model allows us to determine
the current quark masses**.
Other questions that can be addressed using these techniques include
those concerning the properties of the techni-Higgs. This is discussed in
chapter 7. The techni-Higgs may be viewed as a dilaton, or Goldstone
boson associated with spontaneously broken scale invariance. Of course
quantum field theories are not scale invariant, as demonstrated by the case
of massless QCD. Although this theory has no mass scale in the
Lagrangian, the effective coupling constant runs with momentum, so there
is indeed a scale. Such explicit scale invariance breaking would give a mass
to the dilaton. In the case of technicolour theories there has been recent
interest in walking theories, that is theories in which the coupling runs very
slowly. It might be expected that such theories could possess a light
dilaton. By techniques similar to those mentioned above we calculate the
dilaton decay constant.
In chapter 8 we compare our results with those from other techniques,
and summarize our conclusions.
Footnotes for Chapter 1:
* For other examples of Goldstone bosons in condensed matter physics see reference
[3].
** A phenomenological chiral Lagrangian can only determine quark mass ratios.
(Warning! The equations have not been completely converted to html yet, proceed with caution.)
Chapter 2
QCD and Spontaneous Chiral Symmetry Breaking
2.1 - QCD
A major event in the history of particle physics was the development of
quantum chromodynamics (QCD) circa 1972 [8].
QCD describes the
interaction of various flavours of quarks (each of which come in three
colours) with eight, non-Abelian, coloured gauge fields. The QCD
Lagrangian is given by
L_QCD = psibar(x){gamma^µ i partial_µ +g T^a A^a_µ (x) + M}psi(x) - (1/4) F^a_µ nu F^a^µ nu, (2.1)
where the gluon field strength tensor is
F^a_µ nu = partial_µ A^a_nu - partial_nu A^a_µ + g f^abc A^b_µ A^c_nu , (2.2)
and M is the quark mass matrix (flavours and colours are implicitly
summed over). The generators and structure constants of the gauge group
SU(3)colour are denoted by Ta and fabc respectively. This Lagrangian (eq.
2.1) is invariant under local SU(3)colour gauge transformations. In the
limit that the quark masses go to zero, it is also invariant under global
transformations in which the left and right-handed quark flavours are
independently rotated into other flavours by elements of SU(N), where N is
the number of flavours. This SU(N)_L× SU(N)_R symmetry is called a chiral
symmetry. This approximate chiral symmetry was built into QCD in the
hope of successfully reproducing the current algebra results of the 60's.
The discovery of asymptotic freedom in 1973 [9]
gave the new theory
its first great qualitative success. By the start of the 80's, QCD was widely
accepted as the theory of strong interactions. However, almost 20 years
after its inception, QCD has not yet been quantitatively tested by
experiment. This sad state of affairs is not the result of a lack of effort by
experimentalists, but the inability of theorists to make predictions that can
be tested with available machines^1. The problem with (or saving grace of)
QCD is that non-perturbative effects dominate at energies where the most
interesting data is available (~ 1 GeV). Despite this, and for lack of an
alternative theory, QCD is now, more than ever, widely believed to be the
correct theory of strong interactions. Discounting the possibility of exactly
solving QCD, the avenues open to the theorist wishing to investigate strong
interactions at low energies are to analyze QCD numerically with lattice
simulations^2, or to construct models of QCD. In this thesis we will pursue
the latter course.
A reasonable model of QCD is usually required to incorporate two
non-perturbative effects: confinement and spontaneous chiral symmetry
breaking. While (in the massless limit) confinement implies spontaneous
chiral symmetry breaking, the reverse is not necessarily true. In fact
lattice simulations have shown that chiral symmetry breaking in QCD-like
theories can occur at much larger energy scales than the confinement scale
[10]. This lends support to the idea that it may be possible to treat these
two effects separately. For example, Georgi [11]
has argued that the chiral
symmetry breaking scale is roughly 1 GeV, while the conventional
confinement scale is of order 100-300 MeV. In what follows we will
concentrate almost entirely on chiral symmetry breaking.
The presently accepted (current) masses (renormalized at 1 GeV) for
up, down, strange, charm, and bottom quarks are [12]:
m_u = 5.1 ± 1.5 MeV,
m_d = 8.9 ± 2.6 MeV,
m_s = 175 ± 55 MeV,
m_c = 1.35 ± 0.05 GeV, and
m_b = 5.3 ± 0.1 GeV. (2.3)
For most physics below 1 GeV, the heavy quarks (charm and bottom)
should make only a negligible contribution, that is, the first order
approximation is that they are infinitely heavy. The light quarks, on the
other hand, have masses much lighter than the typical hadronic scales (m_rho,
m_proton) and a reasonable first approximation (at least for up and down
quarks) might be to set their masses equal to zero (i.e., take the the chiral
limit). In this limit the QCD Lagrangian has, neglecting the heavy quarks,
an SU(3)_L× SU(3)_R symmetry. Normally we would expect the spectrum of
the theory to reflect the symmetries of the Lagrangian, which would imply
that, for example, vector and axial-vector mesons should have the same
masses, whereas in reality m_rho approx 770 MeV, and m_a1 approx 1270 MeV. The
symmetry that is apparent in the spectrum is the diagonal subgroup SU(3)_V
(the subscript indicates a vector symmetry, since the left and right-handed
quarks are rotated by the same amount) or, as it is more commonly known
SU(3)_flavour. There are three possibilities which explain this discrepancy:
i) QCD is wrong, ii) taking the quark masses to be zero is a bad
approximation, or iii) chiral symmetry is spontaneously broken.
Stubbornly, we will examine the third possibility.
2.2 - Spontaneous Chiral Symmetry Breaking
Spontaneous symmetry breaking refers to the situation where the
ground state (or vacuum) does not enjoy the symmetry of the Lagrangian.
That is, the vacuum is not invariant under a symmetry operation. Through
Goldstone's theorem [2] this implies the existence of massless particles, one
for each broken generator, each with the quantum numbers of the
associated generator. If a small explicit symmetry breaking term is added
to the Lagrangian, the Goldstone bosons (GB's) obtain a small mass. In
our case, there are eight broken axial generators lag5, where la is a
generator of SU(3), so the GB's should be a flavour octet of pseudoscalar
mesons. In reality, the eight lightest hadrons are the pseudoscalar mesons:
pi^±, pi^0, K^±, K,Kbar, and eta. To see how chiral symmetry might be
spontaneously broken in QCD, we will have to take a closer look at non-
perturbative dynamics.
Let us consider the full quark propagator in massless QCD: Sf(p).
Order by order in perturbation theory, chiral symmetry ensures that Sf(p)
has the form
Sf(p) = i/(Z(p) pslash) . (2.4)
However, at low energies we cannot trust perturbative arguments in QCD.
The most general form for Sf(p) allowed by Lorentz and parity invariance
is
Sf(p) = i/(Z(p) pslash - S(p)) , (2.5)
where S(p) is the quark self-energy and S(p)/Z(p) is often referred to as the
dynamical mass (it is often hoped that the dynamical mass is somehow
related to the constituent mass used in non-relativistic quark models). To
go beyond the confines of perturbation theory and determine which form
the quark propagator takes, we turn to the Schwinger-Dyson equations.
The Schwinger-Dyson equations are an infinite set of coupled integral
equations that completely determine the theory^3. The Schwinger-Dyson
equation for the quark propagator (or gap equation^4) is (in Minkowski
space)
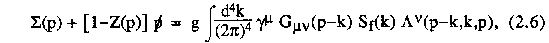
where G_µ nu(p-k) is the full gluon propagator, and Lambda^nu(p-k,k,p) is the full
gluon-quark-quark vertex. This equation is shown pictorially in Figure
2.1. Since S(p) appears on both sides of this equation, it must be solved
self-consistently; this allows for non-perturbative solutions.
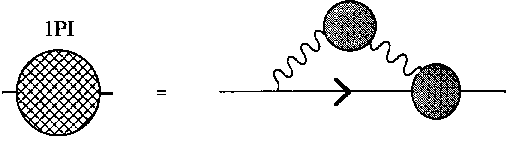
Figure 2.1; The Schwinger-Dyson equation for the one particle
irreducible (1PI) two point function. The straight line represents the full
quark propagator.
Although simple approximations (eg., the ladder approximation [13],
where G_µ nu(p-k) and Lambda^nu(p-k,k,p) are replaced by their tree-order
counterparts) do indeed give non-trivial solutions for S(p), no one has
succeeded in proving that S(p) is non-zero in massless QCD. However,
lattice calculations should be able to determine whether or not S(p) = 0.
The simplest way to do this is to note that the vacuum expectation value
of psibar(x)psi(x) is determined by evaluating a single quark loop using the full
propagator^5. Thus we find that, for one flavour,
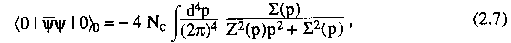
where we have Wick rotated to Euclidean momentum, the 0 indicates the
massless limit, and N_c is the number of colours ( N_c = 3). The importance
of this formula is that S(p) is non-zero if and only if < 0| psibar psi|0> _0 is non-zero. Since psibar psi is not invariant under chiral transformations, either of
S(p) or < 0| psibar psi|0> _0 being non-zero implies that the QCD vacuum itself is
not invariant, that is, chiral symmetry is spontaneously broken. A more
concise way to say this is that S(p) and < 0|psibar psi|0> _0 can be considered to be
order parameters for chiral symmetry breaking.
Current lattice results do indeed suggest that < 0|psibar psi|0> is non-zero in
the chiral limit, and that chiral symmetry is spontaneously broken in QCD
[14].
2.3 - QCD at Low Energies
The idea that chiral symmetry was spontaneously broken was in fact
developed before QCD. Armed only with symmetry arguments, a small
band of theorists in the sixties made an attack on strong interactions. They
attempted to predict various scattering and decay amplitudes using a few
measured parameters. Without a fundamental theory of strong
interactions, one might have expected that they wouldn't get very far.
However, they were remarkably successful: modern theorists have yet to
calculate these amplitudes from QCD with any degree of accuracy. The
point is that chiral symmetry forces Ward-Takahashi (WT) identities upon
the Green functions of the theory, and Goldstone's theorem requires the
existence of light pseudoscalar mesons with a special coupling to
axial-vector currents. If there are no other light hadrons then the GB's dominate
the low energy physics, and measuring a particular amplitude gave
information, through WT identities, on amplitudes with additional low
energy GB's. Thus with current algebra, the PCAC (partially conserved
axial current) hypothesis, and soft-pion theorems^6, theorists were able to
elucidate strong interaction effects without having to understand the
underlying dynamics, indeed without having to assume that a fundamental
Lagrangian even existed^7. Weinberg was the first to point out that a
simpler method for obtaining these symmetry results was to use an
effective Lagrangian [4]. In Weinberg's words [15]:
. . . if one writes down the most general possible Lagrangian,
including all terms consistent with assumed symmetry
principles, and then calculates matrix elements with this
Lagrangian to any given order in perturbation theory, the
result will simply be the most general possible S-matrix
consistent with analyticity, perturbative unitarity, cluster
decomposition and the assumed symmetry principles.
If we are only interested in the interactions at low energies, then we can
concentrate on the GB's, and neglect interactions with more massive
particles. Of course this approximation will break down at large energies,
which suggests that we arrange the effective Lagrangian as an expansion in
powers of the energy (momentum) of the GB's divided by some typical
energy scale of the theory. Terms with higher powers of momentum will
be suppressed if the momentum is less than the typical energy scale. Such
effective Lagrangians based on chiral symmetry are referred to as chiral
Lagrangians.
The only obstacle in the way of immediately writing down a low
energy chiral Lagrangian is that there are an infinite number of
Lagrangians that give the same low energy matrix elements. These
Lagrangians are only distinguished by the manner in which the GB fields
transform under the SU(3)_L× SU(3)_R symmetry. Given an effective
Lagrangian of the GB fields pa, we can invent a new Lagrangian describing
the same physics by defining new fields Pa = pa f(pa), with the only
constraint being that f(0) = 1 (this result goes by the name of Haag's
theorem [5,16]).
Obviously, the thing to do is to choose a GB field that transforms in
some "nice" way. The "nicest" transformation properties were determined
by Coleman, Callan, Wess, and Zumino [5].
They advocated the use of
non-linear realizations of the SU(3)_L× SU(3)_R symmetry. This sounds
extremely complicated, but the underlying idea is quite familiar in the
context of classical mechanics. Given a point particle, we can choose to
describe its position using Cartesian coordinates (x,y,z) or spherical
coordinates (r,theta,phi). If the problem we are solving has a spherical
symmetry, it is easier to use spherical coordinates. The Cartesian
coordinates transform linearly under the rotation group, q and f transform
non-linearly. Thus, spherical coordinates are termed a non-linear
realization of the rotation group.
A standard choice for representing the GB fields is U(x) = exp (-2i pi(x)/F_0 )
where pi(x) equiv lambda^a pi^a(x) (the repeated index is implicitly summed over), and
{lambda^a} are the generators of SU(3) with the normalization Tr(lambda^a lambda^b) = (1/2) delta^ab.
The matrix field U transforms under SU(3)_L× SU(3)_R as U' = LUR&dagger,
where L and R are elements of SU(3)_L and SU(3)_R respectively. With this
choice, the effective low energy Lagrangian for massless QCD is given by
writing down all possible hermitian SU(3)_L× SU(3)_R invariants built out of
U's. The invariants with no derivatives, like Tr(U&daggerU), are constants, so the
first non-trivial term has two derivatives. Thus
L = (1/4) F_0^2 Tr(partial_µ U&daggerpartial^µ U) + . . . , (2.8)
where . . . indicates terms with more derivatives. Expanding in powers of
pa, we find that the lowest order term is 12 partialmpapartialmpa. The factor 14 F_0^2 is
present in equation (2.8) so as to obtain the standard normalization of this
kinetic term. The SU(3)_L× SU(3)_R symmetry of this Lagrangian is
spontaneously broken. A typical ground state is specified by < 0|U|0> = 1,
which is only invariant under SU(3)_V.
External vector (V_µ) and axial-vector (A_µ) gauge fields can be included
by replacing the derivative with a covariant derivative
D_µ U = partial_µ U - i[V_µ + A_µ ] U + iU[V_µ - A_µ ] . (2.9)
By examining the coupling of a pion to an external axial-vector field (i.e.
the pion decay amplitude < 0|J^aµ _5(x)|pi^b(q)> equiv iq^µ F_pi d^ab exp(-iq.x) ) one finds that,
to this order, the pion decay constant F_pi equals F_0 (with our conventions
F_pi approx 93 MeV).
One can also easily include the effects of explicit symmetry breaking,
that is the effects of non-zero quark masses. To do this we consider the
effect on the QCD Lagrangian (eq. 2.1) when the quark fields are
transformed under SU(3)_L× SU(3)_R. The effect is to replace^8 the quark
mass matrix M by L&daggerMR. If M transformed as M' = LMR&dagger, then the QCD
Lagrangian (eq. 2.1), including mass terms, would have a global chiral
symmetry. However, since M does not transform the mass term breaks the
chiral symmetry. This argument shows us how to include explicit
symmetry breaking in the chiral Lagrangian. To first order in M, we can
write down one term that breaks the chiral symmetry, but would be
invariant if M transformed in the prescribed manner [17]. Combining the
two derivative term with this new term (allowing for an undetermined
coefficient B_0) we obtain the chiral Lagrangian to lowest (second) order in
the energy expansion^9:
L_2 = (1/4) F_0^2 {Tr(D_µ U&daggerD^µ U) + 2B_0 Tr(MU&dagger + M&daggerU)}. (2.10)
Since M doesn't transform, this additional term breaks the chiral symmetry
and gives the GB's a mass (often they are then referred to as pseudo- or
almost-Goldstone bosons.). To see this explicitly we can expand equation
2.10 in powers of pa and read off the mass terms. To this order we find
(for simplicity we take mu = md = m ) :
M_pi^2 = 2 m B_0 ,
M_K^2 = (m + m_s) B_0 ,
M_eta^2 = (2/3) (m + 2 m_s) B_0 . (2.11)
where the mass eigenstates have been suggestively named based on their
implied quark content. These are just the standard Gell-Mann-Oakes-
Renner [18] mass formulae if we identify < 0|psibar psi|0> _0 with -F_0^2 B_0. As
expected the GB masses vanish as the quark masses approach zero. The
functional form of this dependence has been verified in lattice calculations
[6]. This result also shows why it was consistent to keep terms of second
order in momentum and first order in quark masses. Near the GB mass
shell p2 approx M2GB ~ mquark B_0, so in the energy expansion one quark mass is of
the same order as two derivatives. The mass formulae also give the
Gell-Mann-Okubo mass formula [19]
M_eta^2 = (1/3) (4 M_K^2 - M_pi^2) . (2.12)
This is all very reassuring. However the reason that chiral Lagrangians
are useful is not that they can reproduce known current algebra results, but
that they offer a systematic method for calculating the higher order
corrections to these results. To go to the next order in the energy
expansion one simply lists all possible terms with up to four derivatives or
two powers of quark masses. In the notation of Gasser and Leutwyler
(G&L) [20] the next to leading order (fourth order) terms are^10
L_4 = L1 {Tr(D_µ U&daggerD^µ U)}2 + L2 Tr(D_µ U&daggerD_nuU)Tr(D^µ U&daggerD^nU)
+ L3 Tr(D^µ U&daggerD_µ UD^nuU&daggerD_nuU)
+ L4 Tr(D_µ U&daggerD^µ U)Tr(chiU&dagger + chi&daggerU)
+ L5 Tr(D_µ U&daggerD^µ U(U&daggerchi + chi&daggerU))
+ L6 {Tr(chiU&dagger + chi&daggerU)}2 + L7 {Tr(chi&daggerU - chiU&dagger)}2
+ L8 Tr(chi&daggerUchi&daggerU + chiU&daggerchiU&dagger)
- iL9 Tr(F^R_µ nuD^µ UD^nuU&dagger + F^L_µ nuD^µ U&daggerD^nuU)
+ L10 Tr(U&daggerF^R_µ nuUF^L^µ nu) (2.13)
where Tr indicates a trace and
chi = 2 B_0 M,
F^R_µ nu = partial_µ R_nu - partial_nuR_µ - [[R_µ ,R_nu],
F^L_µ nu = partial_µ L_nu - partial_nuL_µ - [[L_µ ,L_nu],
R_µ = V_µ + A_µ ,
L_µ = V_µ - A_µ . (2.14)
We have also dropped GB independent terms which are necessary for
renormalization.
Thus the chiral Lagrangian to fourth order in the energy expansion is
given by
L_chi = L_2 + L_4 + L_WZ , (2.15)
where L_WZ is the Wess-Zumino term [25], which is required to reproduce
the effects of anomalies.
The revival of interest in chiral Lagrangians in the 80's was largely due
to the work of G&L [20,21] who determined the fourth order coefficients
by comparison to experiment. They also calculated loop corrections to the
same order. The loop corrections raise an interesting point: the
Lagrangians L_2 and L_4 are not renormalizable which leads to the necessity
of an infinite number of parameters to describe the theory. Fortunately, as
Weinberg showed, the one-loop corrections involving vertices from L_2 are
of order p^4 (i.e. the same order as tree graphs from L_4). In general each
loop adds an additional power of p^2. Thus to renormalize one-loop graphs
from l2, we will need counter-terms of order p^4, but since L_4 contains all
the possible terms allowed by chiral symmetry, we must be able to absorb
the counter-terms in redefinitions of the coefficients of L_4. This means that
the chiral Lagrangian is renormalizable order by order in the energy
expansion.
The result of the efforts of G&L is that more accurate predictions can
be made using chiral perturbation theory for a variety of low energy
phenomena. For example, they use information independent of the s-wave
and p-wave scattering lengths to determine L1 through L10. This
information allows them to calculate the corrections to the standard
Weinberg (order p2) scattering lengths. The corrections bring the chiral
Lagrangian scattering lengths into even closer agreement with experiment.
What does the success of chiral Lagrangians tell us about QCD? Most
importantly it tells us that lQCD has the correct symmetry. Chiral
perturbation theory also enables us to determine the light quark mass
ratios^11, but unfortunately tells us nothing further about QCD. To see
why, let us review the assumptions that lead to the chiral Lagrangian.
Consider a Lagrangian L = L_0 + L_SB which has the following properties:
1. L_0 has an SU(3)_L× SU(3)_R symmetry;
2. the ground state of L_0 is only invariant under SU(3)_V;
3. the symmetry breaking term L_SB is parametrized by a 3x3
matrix M, which, if allowed to transform as M' = LMR&dagger, would
render L_SB invariant; and
4. in the limit M --> 0, the only massless particles in theory are the
eight Goldstone bosons.
Such a Lagrangian can be approximately described at low energies by the
chiral Lagrangian^12 L_chi = L_2 + L_4. At low energies the only discernible
differences between alternative underlying Lagrangians are the values of
the low energy parameters F_0, B_0, L1, . . ., L10. Thus, short of calculating
these coefficients from QCD, chiral perturbation theory cannot distinguish
between QCD and other theories with spontaneously broken chiral
symmetry. The next best thing would be to derive the low energy
parameters from a QCD inspired model. This is what we endeavor to do
in the succeeding chapters.
Chapter 3
Footnotes for Chapter 2:
^1 Although QCD will be tested at HERA.
^2 This entails waiting for much more powerful computers to achieve a reasonable accuracy, and the
possibility of little physical insight into how the theory actually works.
^3 To demonstrate this, one can derive the Schwinger-Dyson eqs. by canonical quantization, and then derive
the path integral formulation from the Schwinger-Dyson eqs. [22].
^4 This name refers to the analogous eq. found in the BCS theory of superconductivity [23].
^5 This is strictly true only in the massless limit. In the massive case < 0 |psibar psi| 0> depends upon
renormalization conventions.
^6 For a review of current algebra see reference [24].
^7 At the time, Lagrangians were out of fashion, and it was widely suspected that it was impossible to
describe strong interactions using a Lagrangian formalism.
^8 To see this, rewrite the quark mass term in terms of left and right-handed quarks, i.e., as psibar_L M psi_R + psibar_R M&dagger psi_L.
^9 We follow the conventional parametrization due to Gasser and Leutwyler.
^10 G&L use the lowest order equations of motion to express an eleventh possible invariant in terms of the
others [20].
^11 Note that chiral Lagrangians cannot determine the scale of the quark masses. Given values for the quark
masses and B_0, we can scale the masses up by a factor of 2, say, and chiral perturbation theory will give the
same results provided that B_0 is divided by 2.
^12 If the underlying theory has anomalies, then a Wess-Zumino term must be included.